الموجات الكهرومغناطيسية (1)

الموجات الكهرومغناطيسية (1)

الموجات الكهرومغناطيسية (1):

معادلات الموجة و الحلول بالإحداثات الكارتيزية :
نشأت معادلات الموجة للموجات المهمة التي لا تحمل أي شحنة بافتراض أن كثافة الشحنة تساوي صفر كما أنه يفترض أن المواد خطية و موحدة الخواص مثل : موجات الراديو.
عالجت معادلات الموجة معادلة ماكسويل للفيض الكهربي والتي تُوضح بالقانون :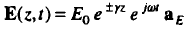

وبالنسبة لمعالجة معادلة الموجة لمعادلة ماكسويل للفيض المغناطيسي والتي تُوضح بالقانون :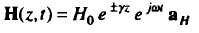

حيث أن متجها الوحدة (aH/aE) هما محددان و متعامدان وليس لهما مركبة في إتجاه الانتشار.
الموجات المستوية لها (E/H) متعامدان علي إتجاه الإنتشار.
الانتشار في أوساط مختلفة :
بما إن ثابت الانتشار لموجة مستوية يعتمد علي :μ/€/σ
يكون الحل لمعادلة الموجة للفيض الكهربي هو إخفاء الاعتماد علي الزمن فتكون العلاقة :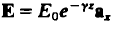

ويكون معادلة الموجة للفيض المغناطيسي :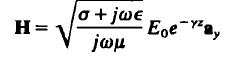

وتعرف الممانعة الذاتية للوسط هي النسبة بين الفيض الكهربي إلي المجال المغناطيسي تُعرض من العلاقة :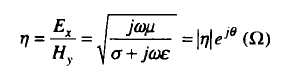

ثابت الانتشار و الممانعة الذاتية في حالة أن المواد في جالة توصيل جيدة حيث أ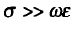ن () فتكون :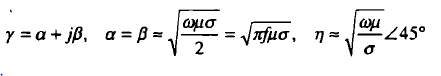

كل موصلات الموجات تتوهن من خلال العمق السطحي الذي عنده تتوهن قيمة المجال تتوهن إلي 37 % من قيمته الأصلية .

مثال (1) :

مثال (2) :

مثال (3):

المرجع :

sabry mohammed , (2004) , Electromagnetic ,international House for cultural investments

ساعد في نشر والارتقاء بنا عبر مشاركة رأيك في الفيس بوك

الموضوع الأصلي: الموجات الكهرومغناطيسية (1) || الكاتب: أحمد م || المصدر: اسم منتداك

www.domin.com

كلمات البحث

العاب ، برامج ، سيارات ، هاكات ، استايلات

المصدر: منتدى لغة الروح