
|
#1
|
|||||||
|
|||||||
|
ثابت بولتزمان
Disambigua compass.svg ميز عن ثابت ستيفان-بولتزمان. قيمة k الوحدة 1.380×10−23 J K−1 8.617×10−5 eV K−1 1.380×10−16 إرج K−1 للمزيد من التفاصيل انظر قيم ثابت بولتزمان بالوحدات الأخرى في المقالة. ثابت بولتزمان (k or kB) هو أحد الثوابت الفيزيائية وهو يعطي العلاقة بين طاقة الجزيء أو الذرة في الحالة الغازية ودرجة الحرارة. فهو يعطي متوسط طاقة الحركة لكل جزيء أو ذرة في الغاز بمجرد معرفة درجة الحرارة المطلقة للغاز. وهو عبارة عن حاصل قسمة ثابت الغازاتR على عدد أفوجادرو NA : k = \frac{R}{N_{\rm A}}.\, R ثابت الغازات = 8.314 (جول/كلفن/مول) NA = 6,022 ×1023 لثابت بولتزمان نفس وحدات الإنتروبية. وهوثابت يسمى باسم عالم الفيزياء النمساوي لودفيغ بولتزمان. الجزيئات في الحالة الغازية ثابت بولتزمان هو الحلقة بين الجزيئات وخصائص الحالة الغازية. فقانون الغازات يقول في حالة الغاز المثالي أن حاصل ضرب ضغط الغاز P في حجمه V يتناسب مع كمية المادة n ودرجة الحرارة المطلقة T .أي أن: \ pV = nRT, حيث R ثابت الغازات 8.314J K−1 mol−1 (جول/كلفن/مول) وهو يعطي الطاقة الكلية للغاز. وبالتعويض عن k في هذه المعادلة نحصل على النصيب المتوسط لكل جزيئ : p V = N k T \,, حيث N عدد جزيئات الغاز أو عدد الذرات فيه. توزيع الطاقة بين الذرات نفترض وجود غاز معزول تحت درجة حرارة مطلقة T فتحصل كل ذرة في الغاز علي طاقة حركة متوسطة بمقدار kT/2 وذلك لكل اتجاه يمكن للذرة التحرك فيه. وباعتبارنا الذرة نقطة كروية فلها 3 اتجاهات تتحرك فيهم وهي المحاور س، ص وع.وبحسبة بسيطة نصل إلى متوسط طاقة حركة الذرة في الغاز وتكون 5و1 kT ; أي 2.07×10−21 جول أو 0.013 إلكترون فولت (eV) لكل جزيئ عند درجة حرارة الغرفة. توزيع الطاقة بين الجزيئات 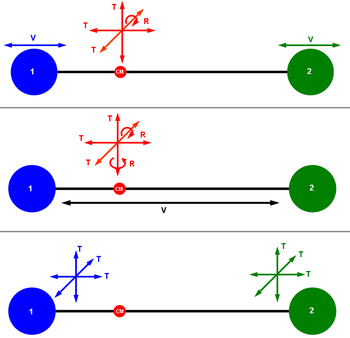 جزيئ ثنائي الذرات، درجات الحركة الحرة: 3 انتقالية + 2 دورانية + 1 اهتزازية. في حالة الغاز المثالي أي في حالة غاز مكون من ذرات منفردة، نقطية الشكل وحجمها مهمل بالنسبة إلى حجم الغاز، تحصل كل إمكانية حركة(درجات حركة حرة) : 3 إمكانيات لحركة الذرات في اتجاه المحاور الثلاثة س، ص، ع مقدارا من طاقة الحركة علي kT /2، فتكون طاقة حركة الذرة : \langle E_{\rm kin}\rangle =\frac{3}{2} k T وبصفة عامة يمكن وضع تلك المعادلة لحالة تكون الغاز من جزيئات، وبفرض أن كل جزيئ له f إمكانية للحركة يصبح متوسط طاقة حركة الجزيئ : \langle E_{\rm kin}\rangle =\frac{f}{2} k T فتكون إمكانية حركة جزيئ مكون من ذرتين هي 3 إمكانيات للحركة في اتجاه الثلاثة محاور، بالإضافة إلى 2 إمكانية حركة دورانية للجزيئ حول مركز الثقل، و1 حركة اهتزازية عبر الرباط، فتكون متوسط طاقة حركة كل جزيئ = \langle E_{\rm kin}\rangle =\frac{6}{2} k T وتزيد درجات حرية الحركة للجزيئات المركبة من 3 ذرات أو أكثر. لهذا نجد أن الحرارة النوعية للماء عالية نسبيا لأن جزيئ الماء مثلث الشكل، وبالإضافة لحركته الانتقالية والدورانية فله عدد كبير آخر من الحركات الاهتزازية (عبر الروابط). وكل درجة حرية تكون طاقتها في ذات القيمة الأسية التي للقيمة kT/2. ومقياس الطاقة هو جول أو إرج أو إلكترون فولت. ساعد في نشر والارتقاء بنا عبر مشاركة رأيك في الفيس بوك المصدر: منتدى لغة الروح |
 |
| مواقع النشر (المفضلة) |
| الكلمات الدلالية (Tags) |
| ثابت, بولتزمان |
|
|
هذا الموقع يستعمل منتجات MARCO1
جميع الحقوق محفوظة لموقع لغة الروح |تصميم المتحدة لخدمات الانترنت